Построить сечение треугольной пирамиды

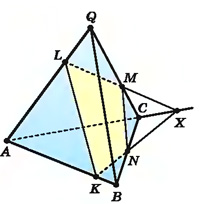
Задача: Построить сечение треугольной пирамиды QABC плоскостью α, проходящей через точки К, L, М ребер AB, AQ, CQ.

Решение:

Секущая плоскость α имеет с гранью AQB две общие точки К и L, поэтому она пересекает эту грань по отрезку KL.

Также, поскольку точки L и М общие точки секущей плоскости и грани AQC, то LM — линия пересечения этих плоскостей.

Грань AВС имеет с секущей плоскостью общую точку К. Найдем точку, в которой плоскость α пересекает ребро ВС. Не забывайте повторять формулы по геометрии. Обратим внимание на то, что точка X пересечения прямых LM и АС принадлежит плоскости α, плоскости AQC и плоскости ABC. А поскольку точки К и X — общие точки плоскостей α и ABC, то КХ — прямая, по которой плоскость α пересекает плоскость ABC. Точка N пересечения прямой КХ с ребром ВС принадлежит плоскости α. Значит, плоскость α пересекает грань ABC по отрезку KN, а грань BQC — по отрезку MN.

Четырехугольник KLMN — искомое сечение пирамиды плоскостью α.

Прямые KL и KN называют следами плоскости α на плоскостях ABQ и ABC соответственно.