Восстановить треугольник по точкам пересечения биссектрис углов треугольника со вписанной в него окружностью

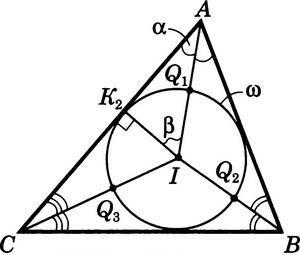
Задача:Q₁,Q₂, Q₃- первые точки пересечения биссектрис углов треугольника ABC  со вписанной в него окружностью w (рис. 5). Восстановите треугольник ABC по точкам Q₁, Q₂, Q₃.

Решение:

Окружность с центром I, описанная около треугольника Q₁Q₂Q₃, совпадает с w. Известно, что

 

Значит, можно построить углы

Соединяем отрезками точки Q_l, Q₂, Q₃ и строим окружность ω. Затем строим точку касания ее со стороной АС: под углом b к отрезку Q₁I проводим через точку I прямую, которая пересекает АС в искомой точке К₂. Аналогично получаем точки касания К₁ и К₃, принадлежащие двум другим сторонам треугольника. Ситуация сведена к рассмотренной ранее задаче -см. тут.