Как построить треугольник на пересечении продолжения высот и описанной около него окружности

Задача: Продолжения высот треугольника ABC пересекают описанную около него окружность ω в точках N₁, N₂, N₃. Постройте треугольник ABC, зная положение точек N₁, N₂, N₃.

 

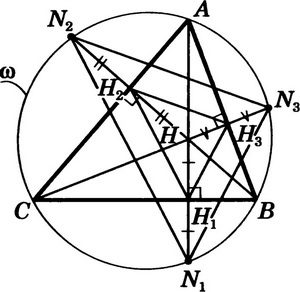
Решение:

Построим треугольник N₁N₂N₃ и опишем около него окружность. Она совпадает с ω. Точки N₁, N₂, N₃ симметричны ортоцентру Н треугольника ABC относительно его сторон (известный факт геометрии треугольника). Поэтому треугольники Н₁Н₂Н₃ иN₁N₂N₃ гомотетичны; центр гомотетии — точка Н, а коэффициент k = 2. Следовательно, биссектрисы углов треугольника N₁N₂N₃ пересекают окружность ω в искомых вершинах А, В, С (см. задачу построение треугольника по основаниям трех его высот).