Определите знак выражения

Числа a, b и c удовлетворяют условиям

(4a + 2b + c)(9a + 3b + c) < 0 и (9a – 3b + c)(16a – 4b + c) < 0. Определите знак выражения (a + b + c) (4a – 3b + c).

Решение:

(№593 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)

Эту задачу можно решить методом перехода к новым переменным.

Пусть с = 0, тогда должна выполняться система неравенств:

Покажем систему на плоскости (a, b).

Из графика видим, что при с = 0 система решений не имеет, значит с ≠ 0. Разделим два неравенства на с ≠ 0:

По условию необходимо найти значение выражения (a + b + c) (4a – 3b + c), поделим и его две части на с ≠ 0 (это не изменит знак выражения):

(a/с + b/с + 1) (4a/с – 3b/с + 1).

Обозначим x= a/с, y = b/с. Исходная система принимает вид:

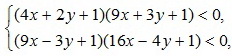
А определить требуется знак выражения (x + y + 1) (4x – 3y + 1).

Построим последнюю систему на плоскости (x, y).

Исходя из графика, делаем вывод, что (x + y + 1) (4x – 3y + 1)>0, т.к. в области, где исходная система имеет решение, выражение, знак которого нужно найти, принимает именно положительные значения.

Ответ: (a + b + c) (4a – 3b + c)>0.

Научиться решать задачи повышенной сложности по теме тождества можно здесь.