Целые части чисел
Докажите, что при любом натуральном значении переменной n целые части чисел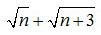 
и 
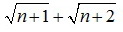равны.
Решение:
(№1506 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)
Эту задачу можно решить,используя метод оценки.
С помощью возведения в квадрат непосредственно можно доказать неравенства:
Поэтому
.
Но
: если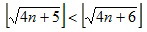 
, то существует натуральное число k, такое, что
, 
, то
но при целых значениях k число k2 не может при делении на 4 иметь в остатке 2:
Это означает, что при любом натуральном значении переменной n целые части чисел 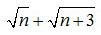и 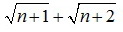равны.