Дробная часть числа

Найдите сумму, где a — некоторое число, натуральные числа b и m взаимно простые, а {x} обозначает дробную часть числа x, это означает разность между x и наибольшим целым числом, которое не превышает x: {x} = x – [x].

Решение:

(№643 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)

Эту задачу можно решить, используя свойства делимости.

Можно сказать, что нам нужно найти.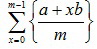

Пусть при некоторых х₁ и х₂ (х₁ > х₂), тогда – целое число. Но не может быть целым, поскольку b и m взаимно простые, а х₁ – х₂ < m, 0 ≤ х₁ ≤ m – 1, 0 ≤ х₂ ≤ m – 1.

Таким образом 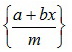принимает m разных значений, которые являются правильными дробями со знаменателем m: 0/m; 1/m; 2/m; … ; (m– 1)/m.

.

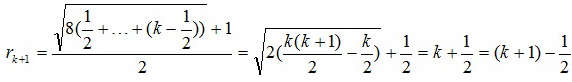Ответ: (m– 1)/2.