Окружность, вписанная в треугольник делит медиану на три части
Окружность, вписанная в треугольник ABC, делит медиану AM на три части. Определите, как сторона BC относится к стороне AB и к стороне CA.
Решение:
(№679 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)
Эту задачу можно решить методом алгебраических и геометрических интерпретаций.
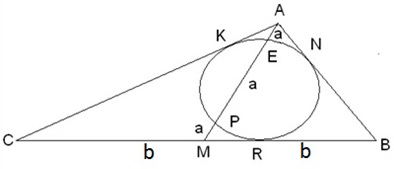
Имеем: AE = EP = PM = a; AK = AN; NB = BR = RC = CK = b.
Поскольку квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то AK2 = 2a·a= 2a2.
Используем формулу для медианы треугольника:
4·АМ2 = 2·(АС2 + АВ2) – СВ2,
4·(3·a)2 = 2·((2·(2)1/2·a + b)2 + b2) – (2·b)2,
20·a2= 8·(2)1/2·a·b.
Последнее равенство разделим на 4·a ≠ 0, получим: 5·a = 2·(2)1/2·b, откуда a = (2·(2)1/2·b)/5.
Выразив все стороны треугольника через b, получим следующее:
ВС:АВ:СА = (2b):(b):( 2·(2)1/2·a + b) =
= = 10:5:13.
= 10:5:13.
Ответ: 10:5:13.
Решения задач про окружность.