Окружности помещены внутри параболы

Окружности w₁, w₂, w₃, ... помещены внутри параболы y = x² так, что w₁ касается параболы в ее вершине и имеет радиус 0,5, окружность w_{т + 1} при каждом m касается окружности w_m и ветвей параболы. Найти радиус окружности w₂₀₀₉.

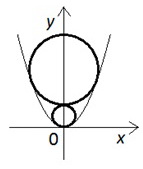
Решение:

(№641 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)

Эту задачу можно решить, используя метод индукции.

Пусть r_n – радиус окружности w_n, S_n = r₁ + r₂ + … + r_n.

Тогда уравнение окружности w_{т + 1}  имеет вид:

x² + (y– (2S_n+ r_n+1))² = r_n+1².

Условие касания означает, что уравнение y + (y– (2S_n+ r_n+1))² = r_n+1² имеет единственный корень, тогда его дискриминант:

D = (2r_n+1–1)² – 8S_n = 0.

r_n+1 = ((8S_n)^1/2 + 1)/2, поскольку r_n+1> 0.

Откуда r₂ = 3/2, r₃ = 5/2.

Индукцией можно убедиться, что r_n = n – 1/2.

Действительно, если r_m = m – 1/2 при m≤k, то

.

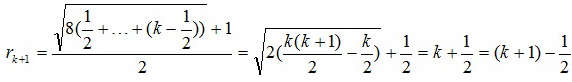Значит, r₂₀₀₉ = 2009 – 1/2 = 2008,5.

Ответ:r₂₀₀₉ = 2008,5.