Вписанная в треугольник окружность

Точки A₁ и C₂, B₁ и A₂, C₁ и B₂ выбраны соответственно на сторонах AC, AB и BC треугольника ABC так, что A₁A₂||BC, B₁B₂||AC, C₁C₂||AB и отрезки A₁A₂, B₁B₂, C₁C₂ пересекаются в центре окружности, вписанной в треугольник ABC. Найдите значение выражения

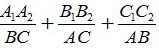
Решение:

(№235 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)

Эту задачу можно решить методом алгебраических и геометрических интерпретаций.

BC₂ОA₂, CB₂ОA₁, AB₁ОC₁ – параллелограммы.

ΔОС₂В₂ и ΔАВС; ΔОА₂В₁ и ΔАВС; ΔС₁ОА₁ и ΔАВС – подобные треугольника (по 3 углам) (*). Тогда выполняются следующие неравенства:

 (выполняется (*), то ) ==

= (BA₂+ B₁A+ B₁A₂ = AB) = 3 – 1 = 2.

Ответ: 2.

На сайте мы  предлагаем правильное и подробное решение нестандартных уравнений и неравенств.