Точка пересечения высот треугольника

В прямоугольном треугольнике ABC проведена высота CD к гипотенузе. Докажите, что перпендикуляр, опущенный из точки A на медиану CM треугольника BCD, делит отрезок CD пополам.

Решение:

(№322 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)

Эту задачу можно решить методом внутренней симметрии.

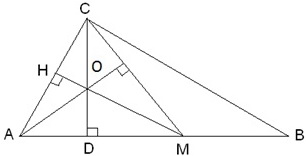
Поскольку О – точка пересечения высот треугольника АСМ, то ОМ – перпендикуляр к АС.

Рассмотрим ΔАСМ. Поскольку ВС┴АС и МН┴АС, то МН||ВС. Поскольку СМ – медиана ΔСDB, то DМ = МВ, но МО||ВС, это означает, что МО – средняя линия ΔСDB, и СО = ОD, что и требовалось доказать.

Также на сайте можно найти решение других олимпиадных задач для школьников.