Решить в целых числах уравнение
Решить в целых числах уравнение 3(x2 +xy +y2) = x + 8y.
Решение:
(№1093 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)
Эту задачу можно решить методом сведения к квадратному уравнению.
Сгруппируем члены уравнения следующим образом:
3x2 + x (3y – 1) + 3y2 – 8y = 0.
Решения последнего уравнения существуют, если его дискриминант – неотрицательное число: D = 9y2 – 6y + 1 – 36y2 + 96y≥ 0, 27y2 – 90y – 1 ≤ 0.
Решая последнее неравенство, получаем, что 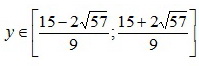 .
.
Целые числа, которые лежат между числами  и
и  : 0; 1; 2; 3.
: 0; 1; 2; 3.
Непосредственной подстановкой в исходное уравнение вместо y значений 0; 1; 2; 3, получаем, что при y1 = 0 x1 = 0, при y2 = 0 x2 = 0. Когда подставляем вместо y 2 и 3, получаем, что число x — нецелое число. Таким образом целые решения уравнения – (0; 0); (1; 1).
Ответ: (0; 0); (1; 1).