Три медианы треугольника пересекаются в одной точке
Теорема: Три медианы треугольника пересекаются в одной точке, и каждая из них делится точкой пересечения в отношении 2:1, если считать от вершины.
Доказательство:
Пусть медианы MB и РА треугольника MNP пересекаются в точке О.
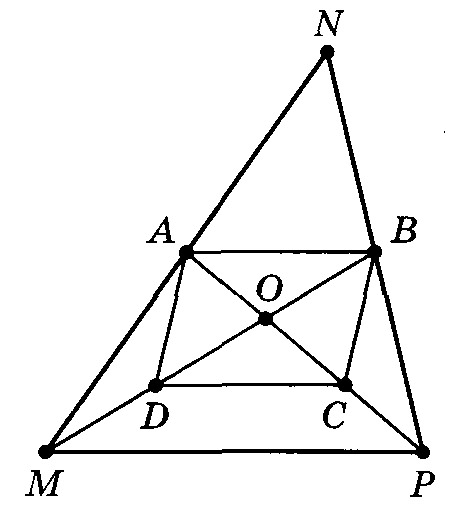
Найдем середины С и D отрезков ОР и ОМ и рассмотрим четырехугольник ABCD. Его стороны АВ и DC параллельны и равны как средние линии треугольников MNP и МОР с общей стороной MP. Поэтому четырехугольник ABCD — параллелограмм.
Поскольку диагонали параллелограмма точкой пересечения делятся пополам, то OD = ОВ. Учитывая, что D — середина отрезка ОМ, получаем MD = OD = ОВ. Значит, МО:ОВ = 2:1. Также РО:ОА = 2:1.
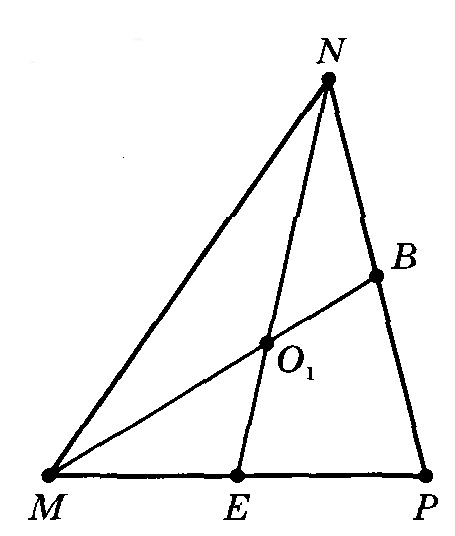
Остается доказать, что третья медиана NE проходит через точку О. Пусть медианы NE и MB пересекаются в точке О1. Тогда по доказанному М01: О1В = 2:1. Учитывая, что и МО:ОВ=2:1, заключаем, что точки 01 и О делят отрезок MB в одном и том же отношении. А это значит, что точка 01 совпадает с точкой О. Значит, медиана NE проходит через точку О пересечения медиан MB и РА.