Как построить график модуля функции и график корня

График и свойства функции у = │ах│ (модуль)

Рассмотрим функцию у = │ах│, где а - определенное число.

Областью определения функции у = │ах│, является множество всех действительных чисел. На рисунке изображены соответственно графики функций у = │х│, у = │ 2х │, у = │х/2│.

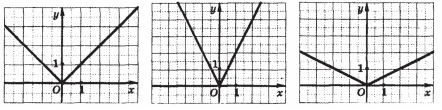
Можно заметить, что график функции у = | ах | получается из графика функции у = ах, если отрицательную часть графика функции у = ах (она находится ниже оси Ох), отразить симметрично этой оси.

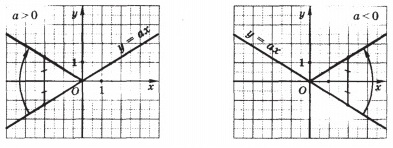
По графику легко усмотреть свойства функции у = │ ах │.

При х = 0, получаем у = 0, то есть графику функции принадлежит начало координат; при х = 0, получаем у > 0, то есть все  другие точки графика лежат выше оси Ох.

Для противоположных значений х, значения у будут одинаковыми; ось Оу это ось симметрии графика.

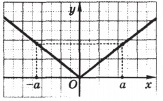
К примеру, можно построить график функции у = │х³│. Чтобы сравнить функции у = │х³│и у = х³, составим таблицу их значений при одинаковых значениях аргументов.

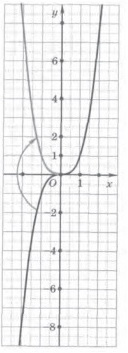Из таблицы видим, что для того, чтобы построить график функции у = │х³│, можно начать с построения графика функции у = х³. После этого стоит симметрично оси Ох отобразить ту его часть, которая находится ниже этой оси. В результате получим график, изображенный на рисунке.

График и свойства функции у = x^1/2 (корень)

Рассмотрим функцию у = x^1/2.

Областью определения этой функции является множество неотрицательных действительных чисел, так как выражение x^1/2 имеет значение только при х > 0.

Построим график. Для составления таблицы ее значений используем микрокалькулятор, округляя значения функции до десятых.

После нанесения на координатную плоскость точек, и плавного их соединения, получаем график функции у = x^1/2.

Построенный график позволяет сформулировать некоторые свойства функции у = x^1/2.

При х = 0, получаем у = 0; при х > 0, получаем у > 0; график проходит через начало координат; остальные точки графика расположены в первой координатной четверти.

Теорема. График функции у = x^1/2 симметричен графику функции у = х², где х > 0, относительно прямой у = х.

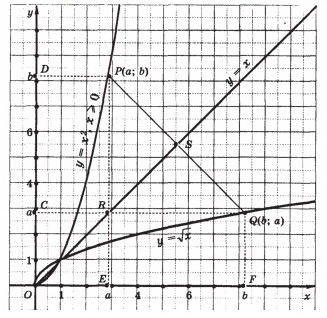
Доказательство. Графиком функции у = х², где х > 0, является ветвь параболы, расположенная в первой координатной четверти. Пусть точка Р (а; b) — произвольная точка этого графика. Тогда истинно равенство b = а². Поскольку по условию число а неотрицательное, то истинно также и равенство а = b^1/2. А это означает, что координаты точки Q (b; а) превращают формулу у = x^1/2 в истинное равенство, или иначе, точка Q (b; а) принадлежит графику функции у = x^1/2.

Так же доказывается, что если точка М (с; d) принадлежит графику функции у = x^1/2, то точка N (d; с) принадлежит графику у = х², где х > 0.

Получается, что каждой точке Р (а; b) графика функции у = х², где х > 0, соответствует единственная точка Q (b; а) графика функции у = x^1/2  и наоборот.

Остается доказать, что точки Р (а; b) и Q (b; а) симметричны относительно прямой у = х. Опустив перпендикуляры на координатные оси из точек Р и Q, получаем на этих осях точки Е (а; 0), D (0; b), F (b; 0), С (0; а). Точка R пересечения перпендикуляров РЕ и QC имеет координаты (а; а) и поэтому принадлежит прямой у = х. Треугольник PRQ является равнобедренным, так как его стороны RP и RQ равны │ b – а│ каждая. Прямая у = х делит пополам как угол DOF, так и угол PRQ и пересекает отрезок PQ в определенной точке S. Поэтому отрезок RS является биссектрисой треугольника PRQ. Поскольку биссектриса равнобедренного треугольника является его высотой и медианой, то PQ ┴RS и PS = QS. А это означает, что точки Р (а; b) и Q (b; а) симметричные относительно прямой у = х.

Поскольку график функции у = x^1/2 симметричен графику функции у = х², где х > 0, относительно прямой у = х, то графиком функции у = x^1/2 является ветвь параболы.