Полуокружность с диаметром AB

Есть полуокружность с диаметром AB. На диаметре выбрана отличная от центра O точка  M, а на полуокружности — такие точки C и D, что AMC = BMD. Найдите CD, учитывая, что CM – MD = l и OM = k∙OA.

Решение:

(№771 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)

Эту задачу можно решить методом внутренней симметрии.

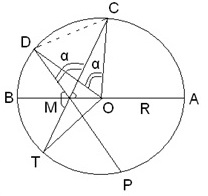
Учитывая условие и то, что СМ∙МD = R² – OM², имеем:

МD(МD – l) = R²(1 – k²), МD² + МD∙l – R²(1 – k²) = 0.

МD =, СМ =

ﮮDМС = ﮮDОС (потому что ﮮDОС = ᴗDС, ﮮDМС = (ᴗDС + ᴗТР)/2 = ᴗDС).

Рассмотрим ΔDМС:

DС² = DМ² + МС² – 2∙DМ∙МС∙cosα =

= (DМ – МС)² + 2∙DМ∙МС∙(1 –cosα) = l² + 2∙R²(1 – k²)∙(1 –cosα). (*)

Рассмотрим ΔDОС: DС² = R² + R² – 2∙R²cosα = 2∙R(1 –  cosα). (**)

С учетом (*) и (**) получаем, что DС = l/k.

Ответ: DС = l/k.