Геометрический способ решения уравнения

Решить уравнение

+  + = 5.

Решение:

(№ 644 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)

Эту задачу можно решить методом алгебраических и геометрических интерпретаций.

Рассмотрим прямоугольный треугольник ABC с катетами AC = 3 и BC = 4. Разделим прямой угол на три равные части и отложим на полученных лучах отрезки CM = x, CN = y (если x и y отрицательные, то они откладываются в противоположную сторону)

Согласно с теоремой косинусов, слагаемые в левой части соответственно равны AM, MN, NB:

= AM, = MN, =NB.

Поскольку AM + MN + NB = AB, то звенья ломаной AMNB расположены на одной прямой.

Это означает, что точки M и N расположены на гипотенузе AB, причем x = CM – биссектриса в треугольнике ACN, а y = CN – биссектриса в треугольнике BCM.

Получаем, что:, откуда.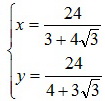

Ответ: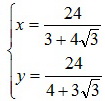.