Матричный метод
Решить данную систему линейных уравнений, используя матричный метод 
Решение:
Для решения системы матричным методом обозначим:
А = 
- основная матрица системы;
Х = 
- столбец неизвестных; В = 
- столбец свободных членов.
Тогда систему из условия можно записать в виде: A*X = B, откуда X = A-1 B, где A-1 – обратная матрица для матрицы А.
Найдем обратную матрицу исходя из формулы:
A-1 = 1 / ∆ 
.
Где Aij –алгебраические дополнения к соответствующим элементам aij матрицы А; а Aij = (–1)i+j Mij, где Mij – миноры, соответствующие элементам aij матрицы А.
∆ = 
= 9 + 8 + 24 -12 - 6 - 24 = -1.
Для вычисления определителя использовали правило треугольника. Так как определитель ∆ отличен он нуля, то существует обратная матрица A-1. Вычислим алгебраические дополнения для каждого элемента основной матрицы системы.
А11 = (–1)1+1 
= + (9 – 6) = 3; А12 = 0; А13 = 4;
А21 = (–1)2+1 
= – (3 – 1) = –2; А22 = –1; А23 =–3;
А31 = (–1)3+1 
= + (– 6 – (–3)) = –3; А32 = –2; А33 = –5.
Получается, что обратная матрица имеет вид А-1 = (–1)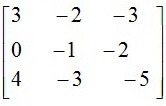
.
Найдем столбец неизвестных по формуле X = A-1 B =
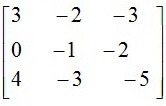= (–1) *= (–1)
= 
.
Здесь использовано правило умножения матриц.
Ответ: х1 = – 8, х2 = – 4, х3 = – 13.
Другие способы решения систем линейных уравнений.