Выяснить, что представляет собой геометрическое место точек,

Решим теперь следующую задачу. Выяснить, что представляет собой геометрическое место точек, из которых данный отрезок ВС длины а виден под заданным углом α.

То, что отрезок ВС длины а и угол а заданы, будет означать для нас, что они изображены на плоскости. Ответ на поставленный вопрос можно найти с помощью следующего чертежного эксперимента. Отметим на плоскости две точки В и С (рисунок). Возьмем произвольный угол (вырежем его из бумаги или воспользуемся одним из углов треугольника для черчения) и, заставив его стороны скользить по точкам А и В, будем отмечать положения вершины. Если наносить на бумагу положения вершины угла аккуратно и достаточно часто, то можно заметить, что полученные точки располагаются на кривой, очень похожей на окружность (см. рисунок).

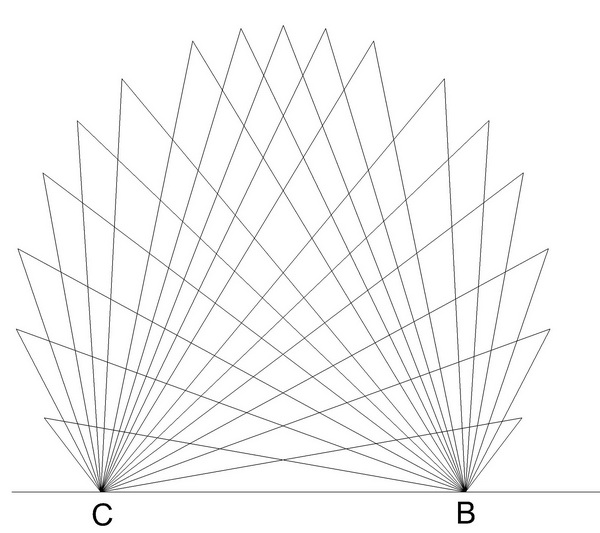
А может быть, искомое множество точек и будет дугой окружности? Зафиксируем одно из положений вершины угла в точке А и опишем вокруг треугольника ABC окружность (рисунок). Тогда, в силу упомянутой выше теоремы, из рисунка любой точки большей дуги этой окружности отрезок ВС будет виден под углом а. (Для простоты, меньшая дуга рассматриваемой окружности на рисунке отсутствует.)

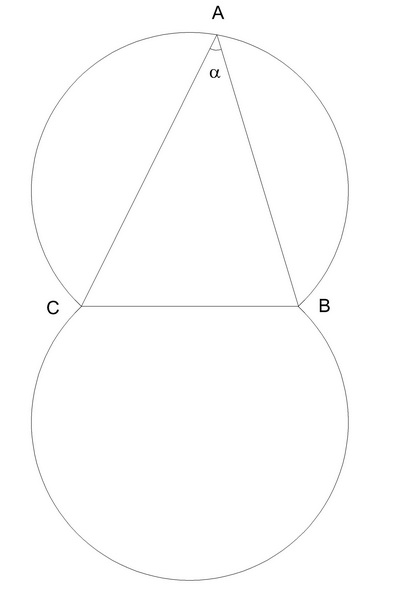
Если отразить большую дугу окружности симметрично относительно прямой, проходящей через точки В и С, то получим еще одну дугу, из каждой точки которой отрезок ВС виден под заданным углом а. Можно ли уже утверждать, что мы нашли все точки плоскости, из которых отрезок ВС виден под углом а? Пока что, нет. Нами показано лишь то, что найденные точки удовлетворяют условию задачи. А существует ли еще хотя бы одна точка, не лежащая на двух найденных дугах, из которой отрезок ВС также виден под углом а?

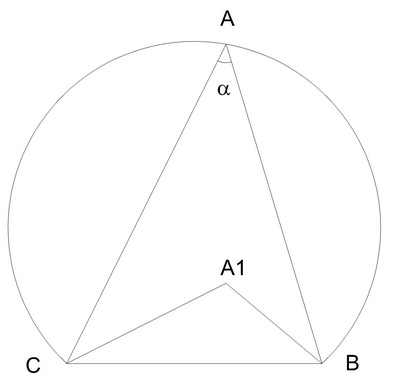
Если бы такая точка А1, лежала внутри окружности, то нашлась бы точка А2, лежащая на построенной окружности такая, что точка А1, лежала бы внутри треугольника А2ВС, и тогда в силу леммы угол ВА1С был бы больше угла ВА2С, т. е. угла α (рисунок). Если бы такая точка А1 находилась за пределами окружности, то на окружности нашлась бы такая точка А2 (рисунок), которая лежала бы внутри треугольника BA1С, и, следовательно, в силу леммы угол ВА1С был бы меньше угла ВА2С, равного α. А это и означает, что никакие другие точки плоскости не удовлетворяют условию задачи. Таким образом, к перечисленным выше г.м.т. мы можем присоединить еще одно.

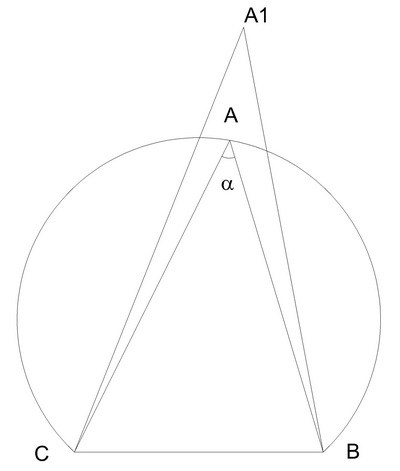
Г.м.т., из которых данный отрезок длины а виден под углом а, есть две одинаковые, симметрично расположенные относительно данного отрезка дуги окружностей, проходящих через концы этого отрезка. В частности, г.м.т., из которых данный отрезок виден под прямым углом, есть окружность, описанная около этого отрезка, как около диаметра.

Заметим, что для построения с помощью циркуля и линейки одной из дуг найденного множества точек достаточно найти хотя бы одну точку А, принадлежащую этой дуге. Сделать это можно, например, с помощью одного из следующих алгоритмов.