На соревнованиях по прыжкам в длину Саша прыгнул дальше Коли и Васи, Коля ближе Васи, но дальше Миши. Кто прыгнул дальше всех, ближе всех?

На соревнованиях по прыжкам в длину Саша прыгнул дальше Коли и Васи, Коля ближе Васи, но дальше Миши. Кто прыгнул дальше всех, ближе всех?

Решение:

 

На множестве детей (Саша, Коля, Вася, Миша) задано отношение «прыгнуть дальше». Требуется упорядочить это множество согласно условиям:

1)  Саша прыгнул дальше Коли;

2)  Саша прыгнул дальше Васи;

3)  Вася прыгнул дальше Коли;

4)  Коля прыгнул дальше Миши. Задачу удобно решать с помощью схемы. Отметим точками детей (С, К, В, М). Будем соединять точки стрелкой, которая обозначает «прыгнул дальше». Получим схему а).

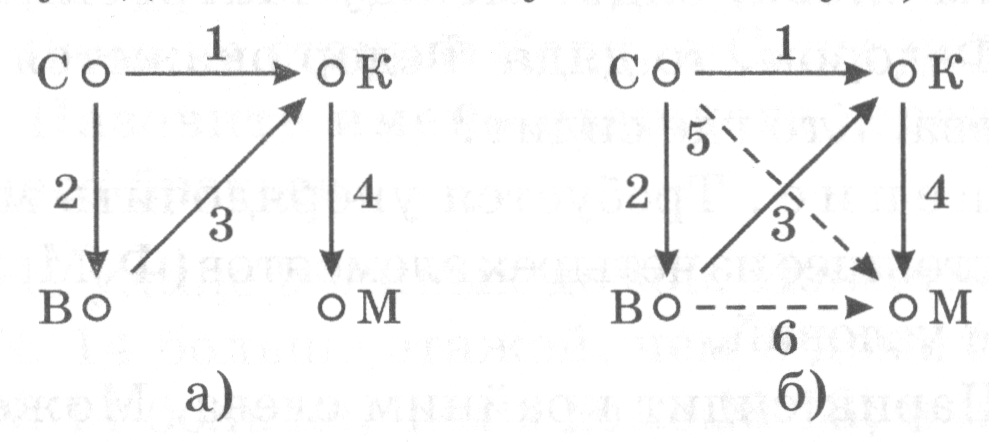
Полученную схему а) можно еще дополнить стрелками, учитывая свойство отношения «дальше»: если Саша прыгнул дальше Коли (стрелка 1), а Коля дальше Миши (стрелка 4), то это означает, что Саша прыгнул дальше Миши. Рисуем стрелку 5. Точно так же: из стрелок 3 и 4 следует стрелка 6. Больше стрелок провести нельзя: каждые две точки соединены стрелкой (схема б).

Теперь будем «читать» схему. Подсчитаем, сколько стрелок выходит из каждой вершины: из С - три стрелки, из В - две, из К - одна, из М - ни одной, сюда стрелки только входят. Так как каждая выходящая стрелка обозначает «прыгнул дальше», делаем вывод, что Саша прыгнул дальше всех, Миша - ближе всех.

Следовательно, множество детей упорядочивается отношением «дальше» так: Саша, Вася, Коля, Миша.