Длины высот треугольника — целые числа

Радиус вписанной в треугольник окружности равен 1, а длины высот треугольника — целые числа. Докажите, что этот треугольник правильный.

Решение:

(№483 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)

Эту задачу можно решить методом алгебраических и геометрических интерпретаций.

Пусть стороны треугольника равны a, b, c.

Тогда 2S = ah_a = bh_b = ch_c = a + b + с, , 1 = .

1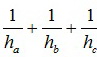) Пусть  h_a < h_b < h_c, тогда 1< 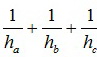, 1< 3/h_a, h_a < 3.

Неравенство треугольника  a< b + c для ,, 1 > 2/h_a, h_a >2, тогда 2 < h_a < 3, но по условию h_a — целое число, значит треугольник не произвольный.

2) Пусть h_a < h_b = h_c. В этом случае получим, как и в случае произвольного треугольника, что h_a— не целое число.

3) Пусть h_a  =  h_b< h_c. В этом случае получим, как и в случае произвольного треугольника, что h_a— не целое число.

4) Остается h_a  =  h_b= h_c. Тогда 1 = 3/h_a, h_a  =  3, то есть h_i — целое число, где i = a, b, c. Это означает, что a = b = c, этот треугольник правильный.

Решай больше задач по математике.