Построить сечение пирамиды

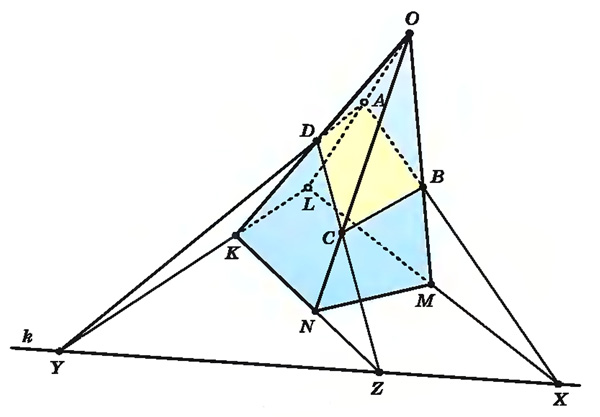
Задача: Построить сечение пирамиды OKLMN плоскостью р, проходящей через точку А на ребре OL и прямую k в плоскости основания KLMN.

Решение:

Вспомним теорию построение сечений многогранников.

Найдем точку X, в которой пересекаются прямые LM и k. Эта точка принадлежит и секущей плоскости β как точка прямой k, и плоскости грани LOM как точка прямой LM. Точка А также принадлежит этим обеим плоскостям. Поэтому плоскость β пересекает плоскость LOM по прямой АХ, а грань LOM — по отрезку АВ, где В - точка пересечения прямых АХ и ОМ.

Так же найдем точки Y и D и отрезок AD, по которым плоскость β пересекает грань OLK, а затем точки Z и С и отрезки DC и ВС. Четырехугольник ABCD — искомое сечение.